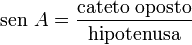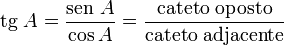Obrigado por visitar meu Blog!!
Espero que tenham gostado!!!
Estudos
quinta-feira, 2 de junho de 2011
quinta-feira, 5 de maio de 2011
Morte de Osama Bin Laden
Morte de Bin Laden é momento crítico para o mundo árabe
Questão é saber se morte de líder da Al-Qaeda estimulará movimentos pró-democracia na região ou alimentará forças extremistas
Nos primeiros dias da primavera árabe, o presidente americano, Barack Obama, frequentemente afirmou a seus assessores que o movimento que tomou conta da região, do Egito ao Iêmen – do lugar onde a Al-Qaeda encontrou suas raízes intelectuais, aquele em que ele se refugiou – criou o que chamou de uma "narrativa alternativa" para uma geração abandonada.

Foto: Divulgação/Casa Branca
Barack Obama durante em uma das reuniões ocorridas neste domingo em que se discutiu a missão contra Osama bin Laden
Não havia fotos de Osama Bin Laden nos protestos de rua, ele observou. Tampouco houve gritos de "Morte à América". A questão agora é saber se a morte de Bin Laden nas mãos de forças especiais americanas e da agência central de inteligência (CIA) estimula o movimento para promover a democracia na região – uma alternativa muito real – ou alimenta as forças islâmicas que agora tentam preencher o vácuo de poder deixado no novo mundo árabe.
A Casa Branca, não surpreendentemente, defendeu na noite de domingo que a morte de Bin Laden veio justamente no momento crucial, quando o mundo árabe vira as costas à ideologia da Al-Qaeda. "É importante notar que é mais adequado que a morte de Bin Laden chegue em um momento em que há grande movimento em direção à liberdade e à democracia no mundo árabe", afirmou um dos assessores de segurança nacional de Obama após o fim do ataque à fortaleza de Bin Laden. "Ele estava em oposição direta ao que os grandes homens e mulheres de todo o Oriente Médio e Norte da África estão arriscando suas vidas para conseguir: direitos individuais e dignidade humana".
Se a Casa Branca de Obama estiver certa na sua interpretação dos acontecimentos, a morte do líder da Al-Qaeda vai representar muito mais do que simplesmente levar justiça ao mentor dos ataques de 11 de setembro de 2001. Ela irá ressaltar o argumento de que o caminho adotado pela Al-Qaeda para mudar o Oriente Médio – através da violência – nunca destituiu um único ditador e nunca trouxe uma mudança real. Por esse motivo, o apelo da Al-Qaeda já estava sumindo antes mesmo de Bin Laden ter seu fim.
Pode também marcar o início de uma nova era em que a guerra global contra o terrorismo, como a administração Bush dizia, deixa de ser a raison d'etre da política externa dos Estados Unidos, como tem sido desde a tarde de 11 de setembro de 2001.
Durante anos, as relações dos Estados Unidos com o mundo foram medidas quase que inteiramente de acordo com a decisão de Washington sobre os países estarem ajudando ou impedindo sua guerra contra o terrorismo. Como candidato, Obama prometeu mudar isso, mesmo que mantivesse uma estratégia contra o terrorismo – e a caçada a Bin Laden – de maneira implacável.
Abordagem
Mas até agora, as esperanças de Obama de levar os Estados Unidos a uma abordagem radicalmente diferente haviam se mostrado mais uma aspiração do que um plano. Ele tentou mudar a atenção dos Estados Unidos para a Ásia, onde está o futuro econômico do país, e buscou reduzir o papel das armas nucleares ao redor do mundo.
Mas os esforços eram sempre sobrepujados pelas questões restantes das "guerras-legado" do Afeganistão e do Iraque: o envio de outros 30 mil soldados ao Afeganistão para evitar que o país se torne um refúgio da Al-Qaeda novamente, a tentativa fracassada de fechar a prisão de Guantánamo, os problemas nas relações com um Paquistão armado com armas nucleares.
Leia também
- Assista ao pronunciamento de Obama
- A morte de Bin Laden em imagens
- Veja onde Bin Laden foi capturado
- Entenda melhor a Al-Qaeda
- Países saúdam EUA por operação
- Imagem de Bin Laden mais velho
- Saiba mais sobre Bin Laden
- Americanos comemoram morte de Bin Laden
- Veja mansão em que Bin Laden estava
- Interpol pede que países reforcem segurança
- Morte de Bin Laden é destaque na imprensa
- Paquistanês narrou ataque a Bin Laden
- Corpo de Bin Laden está no mar, diz imprensa
- Veja antes e depois de Bin Laden
- Morte de Bin Laden nas redes sociais
- Veja quem são os mais procurados pelo FBI
- Exame de DNA mostra ligação com Bin Laden
- Leia as principais notícias sobre Bin Laden
- Obama é maior vitorioso com morte de terrorista
A Primavera Árabe acrescentou um novo e confuso elemento, conforme Washington procurou orientar os eventos que prometiam uma nova relação com uma região que estava derrubando seus ditadores e, talvez, abraçar alguma forma de democracia. Mas como os mais sincero dos assessores de Obama reconhecem, é um movimento que, em sua essência, está fora do controle de Washington.
Agora, a eliminação do símbolo central da Al-Qaeda oferece uma nova oportunidade para que Obama argumente que o grupo não precisa ser uma fixação da política americana. "Até agora, fizemos um bom trabalho em impedir as ações da Al-Qaeda", disse um dos principais conselheiros de Obama este ano, conforme as agências de inteligência secretamente chegavam perto da fortaleza luxuosa em que Bin Laden foi morto nos arredores de Islamabade, no Paquistão. "Mas ainda não não ‘desmantelamos’ o grupo e certamente não o ‘derrotamos’”.
Objetivos
Hoje, Obama pode argumentar que está mais perto de ambos objetivos. De fato, seus assessores alegaram na noite de domingo, que os possíveis sucessores de Bin Laden, incluindo Ayman Al-Zawahri, não têm seu carisma e apelo, e que sua morte vai levar a uma ruptura da organização. A decisão de enterrar o corpo de Bin Laden no mar fez parte de um esforço cuidadosamente calibrado para evitar um túmulo que possa se transformar em um santuário para o líder da Al-Qaida, um lugar onde seus adeptos possam declará-lo um mártir.
Mas nada disso garante que a "narrativa alternativa" frequentemente mencionada por Obama vai acontecer. Com a Irmandade Muçulmana mostrando algum sucesso na sua organização para as próximas eleições no Egito, e os grupos extremistas que esperam lucrar com a guerra civil na Líbia e os protestos na Síria, está longe de ficar claro que as revoluções em curso hoje não serão sequestradas por grupos que têm uma grande afinidade com a ideologia da Al-Qaeda do que com a reforma democrática.
Henry Kissinger observou recentemente que os revolucionários "raramente sobrevivem ao processo da revolução." Geralmente, há uma ‘segunda onda’ que pode desviar o movimento para uma direção diferente”. Se essa segunda onda irá seguir o caminho traçado pelos jovens criadores da Primavera Árabe, ou pelos seguidos de Bin Laden em busca de vingança, pode muito bem determinar se Obama poderá usar a morte de Bin Laden para colocar um fim a uma década sombria.
Foto: AP
Imagem de vídeo divulgada em outubro de 2001 mostra Bin Laden em local não divulgado
*
sexta-feira, 15 de abril de 2011
Trigonometria
Trigonometria (do grego trigōnon "triângulo" + metron "medida") é um ramo da matemática que estuda os triângulos, particularmente triângulos em um plano onde um dos ângulos do triângulo mede 90 graus (triângulo retângulo). Também estuda especificamente as relações entre os lados e os ângulos dos triângulos; as funções trigonométricas, e os cálculos baseados nelas. A abordagem da trigonometria penetra outros campos da geometria, como o estudo de esferas usando a trigonometria esférica.
A trigonometria tem aplicações importantes em vários ramos, tanto como na matemática pura, quanto na matemática aplicada e, consequentemente, nas ciências naturais. A trigonometria é comumente ensinada no Ensino Médio.
Índice[esconder] |
[editar]Sobre a trigonometria
Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais. O fato crucial sobre triângulos semelhantes é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior que o lado do triângulo similar, então o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.
Usando estes fatos, definem-se as funções trigonométricas, começando pelos triângulos retângulos (triângulos com um ângulo reto 90 graus ou π/2 radianos). O maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e devido a soma dos ângulos de um triângulo ser 180 graus ou π radianos, o maior ângulo em um triângulo retângulo é o ângulo reto. O maior lado nesse triângulo, consequentemente, é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são chamados de catetos.
Dois triângulos retângulos que compartilham um segundo ângulo A são necessariamente similares, e a razão entre o lado oposto a A e a hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de A. Este número é chamado de seno de A e é escrito como  . Similarmente, pode-se definir o cosseno (ou co-seno) de A como a razão do cateto adjacente a A pela hipotenusa.
. Similarmente, pode-se definir o cosseno (ou co-seno) de A como a razão do cateto adjacente a A pela hipotenusa.
 . Similarmente, pode-se definir o cosseno (ou co-seno) de A como a razão do cateto adjacente a A pela hipotenusa.
. Similarmente, pode-se definir o cosseno (ou co-seno) de A como a razão do cateto adjacente a A pela hipotenusa.[editar]Círculo Trigonométrico
 Ver artigo principal: Círculo trigonométrico
Ver artigo principal: Círculo trigonométrico
É uma circunferência orientada de raio unitário, centrada na origem dos eixos de um plano cartesiano ortogonal. Existem dois sentidos de marcação dos arcos no ciclo: o sentido positivo, chamado de anti-horário, que se dá a partir da origem dos arcos até o lado terminal do ângulo correspondente ao arco; e o sentido negativo, ou horário, que se dá no sentido contrário ao anterior.
[editar]Seno
 Ver artigo principal: Seno
Ver artigo principal: Seno
Seno é a projeção no eixo vertical do segmento de reta que parte do centro do círculo trigonométrico e vai até a circunferência.
O seno de um ângulo agudo é a razão (divisão) entre a medida do cateto oposto e a medida da hipotenusa.
[editar]Cosseno
 Ver artigo principal: Cosseno
Ver artigo principal: Cosseno
Cosseno é a projeção no eixo horizontal do segmento de reta que parte do centro do círculo trigonométrico e vai até a circunferência.
Como o cosseno é uma projeção, e esta projeção está no interior do ciclo trigonométrico e este possui raio unitário, segue que,  , ou seja, a imagem do cosseno é o intervalo fechado [ − 1,1].
, ou seja, a imagem do cosseno é o intervalo fechado [ − 1,1].
 , ou seja, a imagem do cosseno é o intervalo fechado [ − 1,1].
, ou seja, a imagem do cosseno é o intervalo fechado [ − 1,1].O cosseno de um ângulo agudo é a razão (divisão) entre a medida do cateto adjacente e a medida da hipotenusa.
[editar]Tangente
 Ver artigo principal: Tangente
Ver artigo principal: Tangente
Tangente é o segmento de reta formado entre o ponto de cruzamento de seu eixo com a reta definida pelo centro do círculo trigonométrico e o ângulo com sua origem.
A tangente de um ângulo agudo é a razão (divisão) entre a medida do cateto oposto e a medida do cateto adjacente. A Trigonometria (trigono: triângulo e metria: medidas) é o estudo da Matemática responsável pela relação existente entre os lados e os ângulos de um triângulo. Nos triângulos retângulos (possuem um ângulo de 90º), as relações constituem os chamados ângulos notáveis, 30º, 45º e 60º que possuem valores constantes representados pelas relações seno, cosseno e tangente. Nos triângulos que não possuem ângulo reto, as condições são adaptadas na busca pela relação entre os ângulos e os lados
[editar]Algumas relações
Estas são as mais importantes funções trigonométricas; outras funções podem ser definidas tomando as razões dos outros lados de um triângulo retângulo, mas podem ser expressas em termos de seno e cosseno. São elas a tangente, secante, cotangente, e cossecante.
Até então, as funções trigonométricas tem sido definidas por ângulos entre 0 e 90 graus (0 e π/2 radianos) apenas. Usando um círculo unitário, pode-se estendê-los para todos argumentos positivos e negativos (veja função trigonométrica).
Uma vez que as funções seno e cosseno tenham sido tabuladas (ou computadas por uma calculadora), pode-se responder virtualmente todas questões sobre triângulos arbitrários, usando a lei dos senos e a lei dos cossenos. Estas leis podem ser usadas para calcular os ângulos restantes e lados de qualquer triângulo bem como dois lados e um ângulo ou dois ângulos e um lado ou três lados conhecidos.
Alguns matemáticos acreditam que a trigonometria foi originalmente inventada para calcular relógios de sol, um tradicional exercício em antigos livros. Isto é também muito importante para a agrimensura.
[editar]Teorema de Pitágoras
 Ver artigo principal: Teorema de Pitágoras
Ver artigo principal: Teorema de Pitágoras
O teorema de Pitágoras estabelece que "A soma do quadrado das medidas dos catetos (lados que formam o ângulo de 90°, neste caso a eb) é igual ao quadrado da medida da hipotenusa (lado oposto ao ângulo de 90°, ou c)". Assim: c ² = a ² + b ². Um corolário desse teorema é que se os dois catetos forem de mesmo tamanho, a hipotenusa vale o produto do cateto pela raiz quadrada de 2.
[editar]Aplicações da trigonometria
Existem diversas aplicações da trigonometria e das funções trigonométricas. Por exemplo, a técnica da triangulação é usada em astronomiapara estimar a distância das estrelas próximas; em geografia para estimar distâncias entre divisas e em sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria das funções periódicas, as quais descrevem as ondas sonoras e luminosas.
Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical, acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia,meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogos.
[editar]Fórmulas comuns
Algumas equações envolvendo funções trigonométricas são verdade para todos os ângulos e são conhecidas como "identidades trigonométricas". Muitas expressam relações geométricas importantes. Por exemplo, as identidades Pitagoreanas são uma expressão do Teorema de Pitágoras. Aqui há algumas das identidades mais comumente utilizadas, assim como as fórmulas mais importantes conectando ângulos e lados de um triângulo arbitrário.
[editar]Identidades Trigonométricas
[editar]Fórmula fundamental da trigonometria e seus corolários
[editar]Identidades de soma e subtração
[editar]Fórmulas da duplicação do ângulo
[editar]Fórmulas da divisão do ângulo em dois
Note que 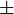 significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.
significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.
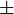 significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.
significa que pode haver qualquer dos dois sinais, dependendo do valor de A / 2.[editar]Identidades triangulares
As identidades que se seguem referem-se a um triângulo com ângulos A, B e C e lados de comprimentos a, b e c, como na figura ao lado. Repare que o lado oposto ao ângulo A é o de comprimento a, o lado oposto ao ângulo B é o de comprimento b e o lado oposto ao ângulo C é o de comprimento c.
[editar]Lei dos senos
 Ver artigo principal: Lei dos senos
Ver artigo principal: Lei dos senos
A lei dos senos para um triângulo arbitrário diz:
ou equivalentemente:
[editar]Lei dos cossenos
 Ver artigo principal: Lei dos cossenos
Ver artigo principal: Lei dos cossenos
A lei dos cossenos (também conhecida como fórmula dos cossenos) é uma extensão do teorema de Pitágoras para triângulos arbitrários:
ou equivalentemente:

- o teorema de pitágoras é um caso particular da Lei dos Cossenos, quando o cosseno de 90°é 0.
[editar]Lei das tangentes
 Ver artigo principal: Lei das tangentes
Ver artigo principal: Lei das tangentes
A lei das tangentes:
'Como saber o ângulo interno de um triângulo rectângulo?'
Sendo
 , em que:
, em que:Sen(A) é comprimento do cateto oposto e Cos(A) A o comprimento do cateto adjacente.
A tangente inversa (tan − 1(A) ou  )é o ângulo interno. sendo assim.
)é o ângulo interno. sendo assim.
 )é o ângulo interno. sendo assim.
)é o ângulo interno. sendo assim.Triângulo retângulo, em geometria, é um triângulo que possui um ângulo reto e outros dois ângulos agudos, para tanto basta que tenha um ângulo reto (90°), pois a soma dos três ângulos internos é igual a um ângulo raso (180°). É uma figura geométrica muito usada na matemática, no cálculo de áreas, volumes e no cálculo algébrico. Em um triângulo retângulo, sabendo-se as medidas de dois lados ou a medida de um lado mais a medida de um ângulo agudo, é possível calcular a medida dos demais lados e ângulos. A área de um triângulo retângulo é dada pela metade do produto dos menores lados.
Se pode considerar um triângulo retângulo como a metade de um retângulo desde que partido pela sua diagonal.
A relação entre os lados e ângulos de um triângulo retângulo é a base da trigonometria.
Índice[esconder] |
[editar]Elementos do triângulo retângulo
Um triângulo retângulo é composto por quatro principais elementos:
- Catetos
- Hipotenusa
- altura relativa à hipotenusa
- projeções dos catetos.
[editar]Catetos
Os catetos são os menores lados do triângulo retângulo. Eles formam o ângulo de 90°.
[editar]Altura relativa à hipotenusa
[editar]Projeções dos catetos
A altura relativa à hipotenusa divide-a em duas partes, denominadas projeções dos catetos.
[editar]Relações métricas do triângulo retângulo
As relações métricas do triângulo retângulo são quatro. Os três triângulos formados são retângulos e semelhantes.
- A hipotenusa é igual à soma das projeções.

Por semelhança de triângulos, temos que:
- O quadrado da altura relativa à hipotenusa é igual ao produto das projeções dos catetos.
- O quadrado de um cateto é igual ao produto entre a sua projeção(que se encontra do seu lado) e a hipotenusa.
- O produto entre a hipotenusa e a altura relativa a ela é igual ao produto dos catetos.
[editar]Teorema de Pitágoras
O Teorema de Pitágoras diz que:
| A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa. | — Pitágoras |
ou, em linguagem matemática:
hipotenusa (AB)² = cateto (BC)² + cateto (CA)²
[editar]Relações trigonométricas do triângulo retângulo
Outra maneira de calcular a medida dos lados de um triângulo retângulo é através da medida de um ângulo e um lado, usando aTrigonometria. As principais relações trigonométricas são: Seno, Cosseno e Tangente. Há outras três: Cotangente, Secante e Cossecante.
[editar]Seno de um ângulo
É dado pela razão entre os lados que formam o outro ângulo agudo, dado pela ordem :
[editar]Cosseno de um ângulo
Cosseno: É a razão entre a medida do cateto adjacente e a medida da hipotenusa e é dado pela razão entre os lados que formam o próprio ângulo agudo, dado pela ordem::
[editar]Tangente de um ângulo
É dado pela razão entre o Seno e o Cosseno de um ângulo, ou entre os catetos, dado pela seguinte ordem:
[editar]Cotangente de um ângulo
É dado pela razão entre o Cosseno e o Seno de um ângulo, ou entre os catetos, dado pela seguinte ordem:
[editar]Secante de um ângulo
É dado pelo inverso do cosseno desse ângulo ou entre os lados que formam o próprio ângulo, dado na seguinte ordem:
[editar]Cossecante de um ângulo
É dado pelo inverso do seno desse ângulo ou entre os lados que formam o outro ângulo agudo, dado na seguinte ordem:
[editar]Ângulos notáveis
[editar]Triângulos retângulos exatos
São aqueles que todos os lados são diferentes dos que formam um terno pitagórico. hipotenusa, cateto, cateto.
[editar]Circunferência inscrita num triângulo retângulo
O diâmetro (d) de uma circunferência inscrita num triângulo rectângulo (a b c) é igual à soma dos catetos, menos a hipotenusa, representado pela seguinte fórmula:
a + b = c + d
- a = cateto
- b = cateto
- c = hipotenusa
- r = raio da circunferência inscrita
- d = diâmetro da circunferência inscrita

Substituindo I e II em III, teremos

Como:
[editar]
Assinar:
Postagens (Atom)
















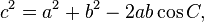
![\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}](http://upload.wikimedia.org/math/8/e/c/8ecc3d7514a107662d79d2b6e0678995.png)
![\frac{b+c}{b-c}=\frac{\tan\left[\tfrac{1}{2}(B+C)\right]}{\tan\left[\tfrac{1}{2}(B-C)\right]}](http://upload.wikimedia.org/math/9/c/6/9c64cb1bc9766cc2165e86b15a300790.png)
![\frac{a+c}{a-c}=\frac{\tan\left[\tfrac{1}{2}(A+C)\right]}{\tan\left[\tfrac{1}{2}(A-C)\right]}](http://upload.wikimedia.org/math/7/6/b/76ba3277c7c47646bac125eaab64e9e4.png)